Αναμενόμενη απόδοση – Επίλογος

Έτσι, ο μέσος όρος αναμενόμενης απόδοσης μακροχρόνια (expected value) που ο παίκτης προσδοκά, θα έχει αρνητική τιμή.

Εάν το κάθε τυχερό παιχνίδι ήταν “δίκαιο” (fair game), δηλαδή δεν υπήρχε ποσοστό παρακράτησης, τότε ο μέσος όρος αναμενόμενης απόδοσης μακροχρόνια θα έπρεπε να ήταν μηδέν. Για να υπολογιστεί η αναμενόμενη απόδοση, απλά πολλαπλασιάζουμε τις πιθανότητες κάθε γεγονότος να συμβεί επί την απόδοση κάθε γεγονότος και στη συνέχεια τα προσθέτουμε συνολικά.

Για να γίνει κατανοητή η έννοια της αναμενόμενης απόδοσης παραθέτουμε τα ακόλουθα παραδείγματα:

Έστω ότι επιθυμούμε να συμμετάσχουμε σ’ ένα παιχνίδι όπου ρίχνοντας ένα νόμισμα, κάθε φορά που θα εμφανίζεται “κεφαλή” θα πληρώνουμε μία μονάδα ενώ κάθε φορά που θα εμφανίζεται “γράμματα” θα πληρωνόμαστε δύο μονάδες.

Επειδή το παιχνίδι θεωρείται “δίκαιο” μια και το γεγονός να έρθει “κεφαλή” είναι ισοπίθανο του γεγονότος να έρθει “γράμματα” (πιθανότητα ½ για το κάθε ένα γεγονός), κατά μέσο όρο μια φορά θα κερδίζουμε και μια φορά θα χάνουμε.

Κάθε φορά όμως που θα κερδίζουμε θα εισπράττουμε 2 μονάδες ενώ κάθε φορά που θα χάνουμε θα δίνουμε -1 μονάδα (αρνητική τιμή εφόσον χάνουμε). Έτσι, κατά μέσο όρο, για κάθε δύο παιχνίδια θα κερδίζουμε 1 μονάδα, ή αλλιώς, κατά μέσο όρο κάθε φορά που παίζουμε θα κερδίζουμε 0,5 μονάδες.

Το ίδιο αποτέλεσμα προκύπτει και από την σχέση:

Α.Α.=1/2*2+1/2*(-1)=1-1/2=1/2,

όπου Α.Α. η Αναμενόμενη Απόδοση.

Ας γνωρίσουμε τώρα πως λειτουργεί η έννοια της αναμενόμενης απόδοσης (Α.Α.) με ένα άλλο παράδειγμα:

Έστω, ότι μας προτείνεται να συμμετάσχουμε σε ένα παιχνίδι όπου θα ρίχνουμε ένα ζάρι όπου για κάθε αποτέλεσμα ισχύουν τα παρακάτω:

1: θα κερδίζουμε 3 μονάδες

2: κανένας δεν θα κερδίζει ούτε θα χάνει

3: θα χάνουμε 5 μονάδες

4: θα κερδίζουμε 3 μονάδες

5: θα χάνουμε 4 μονάδες

6: θα κερδίζουμε 2 μονάδες.

Για να μάθουμε εάν συμφέρει να συμμετάσχουμε στο παιχνίδι με τα παραπάνω δεδομένα, θα πρέπει να υπολογίσουμε την αναμενόμενη απόδοση. Εάν αυτή είναι θετική, τότε είναι υπέρ μας να συμμετάσχουμε. Εάν είναι αρνητική, τότε είναι εις βάρος μας να συμμετάσχουμε. Εάν είναι μηδέν, το παιχνίδι θεωρείται ακριβοδίκαιο.

Με ένα ζάρι, κάθε αποτέλεσμα είναι ισοπίθανο να συμβεί και η πιθανότητα για κάθε αποτέλεσμα είναι 1/6. Έτσι, η αναμενόμενη απόδοση είναι:

Α.Α.=1/6*3+1/6*0-1/6*5+1/6*3-1/6*4+1/6*2=>
Α.Α.=3/6-5/6+3/6-4/6+2/6=>Α.Α.=-1/6

Αρνητική αναμενόμενη απόδοση 1/6 σημαίνει ότι κατά μέσο όρο θα χάνουμε 1/6 μονάδες κάθε φορά που θα παίζουμε, που σημαίνει ότι η συμμετοχή στο παιχνίδι θα αποβεί εις βάρος μας, γιατί σε 600 φορές που θα παίζουμε, αναμένεται να χάσουμε κατά μέσο όρο 600*(1/6)=100 μονάδες, αφού η αναμενόμενη απώλεια κάθε φορά συμμετοχής μας είναι 1/6 μονάδες.

Ο αναγνώστης θα πρέπει να κατανοήσει ότι σε όλα τα τυχερά παιχνίδια, ο κάθε παίκτης συμμετέχει με εις βάρος του πιθανότητες επιστρεφόμενης αναμενόμενης απόδοσης καθώς δεν θα καρπωθεί την πλήρη αναμενόμενη μαθηματική απόδοση σε κάθε κερδοφόρο του στοίχημα, αλλά την μερική απόδοση μια και θα έχει αφαιρεθεί το ποσοστό παρακράτησης.

Όσον αφορά τα παιχνίδια του καζίνο, οφείλει να επιλέξει να συμμετέχει σε παιχνίδια τα οποία έχουν πολύ μικρό Π.Υ.Κ. και κατά το δυνατόν, Π.Υ.Κ. μικρότερο του 3%.

Π.Υ.Κ. 3% σημαίνει ότι το καζίνο, μακροχρόνια προσδοκά να κερδίσει το 3% των χρημάτων από τα κερδοφόρα στοιχήματα. Έτσι, γίνεται αντιληπτό το περιεχόμενο της φράσης “When you win, the casino wins” δηλαδή “Όταν ο παίκτης κερδίζει, το καζίνο κερδίζει”.

Με βάση τα παραπάνω, θα μπορούσαμε να δώσουμε για τον υπολογισμό του Π.Υ.Κ. και τον ακόλουθο τύπο:

Π.Υ.Κ. = 1 – Α.Α. όπου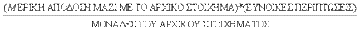

υπενθυμίζοντας ότι, όπως και η σχέση (4), ισχύει για τα στοιχήματα στα παιχνίδια εκείνα όπου το Π.Υ.Κ. είναι σταθερό.

– Στα τυχερά παιχνίδια λειτουργεί ο νόμος των Μεγάλων Αριθμών (The Law of Large Numbers), ή (the Law of Averages).

Ο νόμος αυτός πρωτοπαρουσιάστηκε στις αρχές του 1700 από τον Jakob Bernoulli. Σύμφωνα με τον νόμο αυτόν, ο αριθμός των δεδομένων αποτελεσμάτων (η) ενός γεγονότος ισούται με τον αριθμό των συνολικών αποτελεσμάτων όταν το γεγονός επαναληφθεί (Ν) φορές πολλαπλασιαζόμενο με την πιθανότητα (ρ) να συμβεί το δεδομένο αποτέλεσμα στο γεγονός, όσο το Ν γίνεται όλο και μεγαλύτερο (η=ρ*Ν ή ρ=η/N).

Στα τυχερά παιχνίδια οι πιθανότητες είναι γνωστές και τα ευνοϊκά αποτελέσματα διαιρούμενα με τα συνολικά αποτελέσματα φροντίζουν να εξισώνεται η δεδομένη πιθανότητα όσο ο αριθμός των συνολικών αποτελεσμάτων γίνεται όλο και μεγαλύτερος. Έτσι, εάν συμβολίσουμε με α την αβεβαιότητα η οποία μπορεί να είναι θετικός ή αρνητικός αριθμός, η παραπάνω σχέση γίνεται ρ=η/(Ν+α), και όσο το Ν γίνεται μεγαλύτερο μπορεί να αποδειχθεί ότι το η γίνεται μικρότερο τόσο η αβεβαιότητα αίρεται, έτσι ώστε μπορούμε να ισχυριστούμε ότι το η/Ν προσεγγίζει το ρ όσο το Ν γίνεται μεγαλύτερο. (Στην στατιστική το α συμβολίζεται σ2 και καλείται διασπορά).

Έτσι, για παράδειγμα, στις 1.000 ρίψεις ενός νομίσματος μπορεί να εμφανιστεί 550 φορές κεφαλή και 450 φορές γράμματα, δηλαδή σε ποσοστό 55% αποτέλεσμα κεφαλή και 45% αποτέλεσμα γράμματα. Στο 1.000.000 ρίψεις όμως, σύμφωνα με τον νόμο των Μεγάλων Αριθμών, θα έχουμε περίπου 50% αποτέλεσμα κεφαλή και περίπου 50% αποτέλεσμα γράμματα.

Επίσης, η πιθανότητα να συμβεί ένα γεγονός δεν επηρεάζεται από γεγονότα τα οποία είχαν προηγουμένως συμβεί. Εάν επηρεάζεται, τότε μιλάμε για “δεσμευμένη” πιθανότητα και τα πράγματα διαφοροποιούνται.

– Με την φράση “gambler’s fallacy” εννοούμε την εσφαλμένη πεποίθηση του παίκτη ότι ο νόμος των Μεγάλων Αριθμών έχει ισχύ και μπορεί να εφαρμοστεί και για μικρό αριθμό περιπτώσεων.

Για παράδειγμα, έστω ότι στο παιχνίδι Ρουλέτα, εμφανίστηκε εννέα διαδοχικές φορές, το Μαύρο. Η συνεχής επανάληψη του ίδιου αποτελέσματος για αρκετές διαδοχικές φορές καλείται “βραχυχρόνια τάση”. Εξαιτίας της απόκλισης αυτής προς μια μόνο κατεύθυνση (Μαύρο, Μ, Μ, Μ, Μ, Μ, Μ, Μ, Μ) και σύμφωνα με την “gambler’s fallacy”, ο παίκτης πιστεύει ότι έχει μειωθεί η πιθανότητα να έρθει ξανά το ίδιο αποτέλεσμα και ότι έχει πλέον “ωριμάσει” η πιθανότητα (the maturity of chance – ωρίμανση της τύχης) στην επόμενη ρίψη της μπίλιας να έρθει άλλο αποτέλεσμα, το Κόκκινο.

Το ότι υπάρχει απόκλιση σε μια κατεύθυνση, δεν συνεπάγεται εκτροπή στην αντίθετη κατεύθυνση βραχυπρόθεσμα. Οι αποκλίσεις αμβλύνονται και εξισορροπούνται μακροπρόθεσμα, σύμφωνα με τον νόμο των μεγάλων αριθμών.

Η λύση όσον αφορά το “gambler’s fallacy” είναι να αντιμετωπίζει ο παίκτης κάθε νέο γεγονός ως αυτόνομο, ανεξάρτητο από προηγούμενα γεγονότα ή γεγονότα που θα ακολουθήσουν.

Με την φράση “gambler’s ruin” εννοούμε την πιθανότητα, επιδιώκοντας ο παίκτης να κερδίσει ένα ποσό, να χάσει μακροπρόθεσμα ένα καθορισμένο χρηματικό ποσό που αντιπροσωπεύει το διαθέσιμο κεφάλαιό του, με δεδομένο εκ των προτέρων το στατιστικό πλεονέκτημα που έχει το καζίνο σε κάθε είδος στοιχήματος. Με άλλα λόγια, η φράση υποδηλώνει μετά από πόση χρονική διάρκεια θα χάσει ο παίκτης το περιορισμένο κεφάλαιο που διαθέτει (σε αντίθεση με το καζίνο που διαθέτει σχετικά απεριόριστο κεφάλαιο), εξαιτίας του Π.Υ.Κ. Η φράση συναντάται και ως “risk of ruin”. Όσο μεγαλύτερο είναι το Π.Υ.Κ. τόσο πιο σύντομα θα χάσει ο παίκτης το διαθέσιμο κεφάλαιό του μακροπρόθεσμα.

Για τον λόγο αυτό, ο παίκτης, εκτός του ότι πρέπει να συμμετέχει σε παιχνίδια που έχουν μικρό Π.Υ.Κ., πρέπει εξ αρχής να έχει καθορίσει το “stop-loss limit” δηλαδή το μέρος του χρηματικού ποσού από το διαθέσιμο κεφάλαιό του που εάν το χάσει, θα σταματήσει να συμμετέχει στο παιχνίδι. Το ποσό αυτό μπορεί να είναι από το 20% του διαθέσιμου αρχικού κεφαλαίου έως και όλο το κεφάλαιο.

Για να μην υπάρχουν ασάφειες σχετικά με την κατανόηση του όρου “risk of ruin” θυμίζουμε: Ο παίκτης έχει τη δυνατότητα να κερδίσει βραχυχρόνια. Μακροχρόνια, από τη στιγμή που το Π.Υ.Κ. είναι αναλλοίωτο, πάγιο, σταθερό, αμετάβλητο, ο παίκτης δεν είναι σε θέση να κερδίσει γιατί δεν υπάρχει τρόπος να επιβεβαιώσει ότι ο μέσος όρος όλων των κερδοφόρων στοιχημάτων του θα είναι μεγαλύτερος από τον αντίστοιχο μέσο όρο όλων των χαμένων, με ποσοστά μεγαλύτερα από το Π.Υ.Κ.

– Ένας ακόμα παράγοντας που λαμβάνεται υπόψη για τον υπολογισμό του “κόστους συμμετοχής” του παίκτη σε κάποιο παιχνίδι εκτός του Π.Υ.Κ και του διαθέσιμου κεφαλαίου του παίκτη, είναι και ο δείκτης SM (Standarized Measure) ο οποίος συνδέει την επίδραση του Π.Υ.Κ. και της ταχύτητας (ρυθμού) του παιχνιδιού. Ο ρυθμός ενός παιχνιδιού επηρεάζεται από τον αριθμό των παικτών που συμμετέχουν. Τους παίκτες εξυπηρετεί αργός σχετικά ρυθμός καθώς το “κόστος ανά ώρα συμμετοχής” προκύπτει από το γινόμενο του δείκτη SM επί το διαθέσιμο κεφάλαιο του παίκτη.

Σημαντικός παράγοντας επίσης είναι ο αριθμός και το ύψος των στοιχημάτων.

– Ένας πρακτικός κανόνας για να καθορίσουμε τον αριθμό των κληρώσεων, ρίψεων μπίλιας ή ζαριών κλπ., που απαιτούνται ώστε οι πιθανότητες να είναι “πενήντα-πενήντα” δηλαδή μοιρασμένες στις δύο αντίπαλες πλευρές που συμμετέχουν σε ένα τυχερό παιχνίδι, είναι να πολλαπλασιάσουμε τον αριθμό των δυσμενών περιπτώσεων που αντιστοιχούν σε μία ευνοϊκή, με τον αριθμό 0,7. (b@0,7*Ρ). Ο αριθμός 0,7 είναι η προσέγγιση του αριθμού 0,6931 ο οποίος εκφράζει τον φυσικό λογάριθμο του 2.

Η φόρμουλα καθορισμού του n (break – even point) δημοσιεύτηκε το 1716 στο βιβλίο του Abraham De Moivre “The Doctrine of Chances”. Την αφορμή για τον υπολογισμό του n είχε δώσει αρκετά πιο πριν ο Γάλλος Chevalier de Mere, ο οποίος απευθυνόμενος προς τον Blaise Pascal ήθελε να πληροφορηθεί εάν ήταν υπέρ του οι πιθανότητες εάν στοιχημάτιζε ότι με δύο ζάρια μπορεί να φέρει ζαριά διπλές (2-2) μία φορά στις 24 ρίψεις (ζαριές).

Ένας άλλος τύπος υπολογισμού του b, εάν η πιθανότητα ενός αποτελέσματος είναι (1/α) είναι:

b=[(log2/(log a)-(log(a-1))].

———————————————————–

ΟΡΟΛΟΓΙΑ

Bankroll: Το διαθέσιμο ποσό χρημάτων (κεφάλαιο) που ο παίκτης σκοπεύει να στοιχηματίσει συνολικά.

Cashier’s cage: Ταμείο. Ο χώρος οικονομικών συναλλαγών παικτών-καζίνο.

Casino advantage: Το πλεονέκτημα που έχει το καζίνο έναντι των παικτών σε κάθε παιχνίδι και για κάθε στοίχημα. Εκφράζεται ως ποσοστό παρακράτησης υπέρ του καζίνο. Το ονομάσαμε Π.Υ.Κ. αλλά χρησιμοποιούνται και οι όροι γκανιότα, βιδάνιο. Καλείται επίσης και “house percentage” ή “house edge”.

Casino employee: Το υπαλληλικό προσωπικό του καζίνο.

Casino Manager: Ο Διευθυντής του καζίνο. Έχει την γενική εποπτεία και έλεγχο όλων όσων συμβαίνουν στους χώρους του καζίνο.

Comp (Complimentary): Έξτρα παροχές που είναι σε θέση να προσφέρει το καζίνο στους πελάτες του όπως διαμονή, διατροφή κλπ.

Control room: Ο χώρος όπου βιντεοσκοπείται, καταγράφεται βήμα-βήμα η όλη διεξαγωγή κάθε παιχνιδιού στο καζίνο.

Dealer: Υπάλληλος του καζίνο που χρησιμοποιείται για την διεξαγωγή των παιχνιδιών.

Drop percentage: Το ποσοστό του χρηματικού ποσού του παίκτη που εκτιμά το καζίνο να κερδίσει εξαιτίας του Π.Υ.Κ. Το καζίνο υπολογίζει κατά μέσο όρο να κερδίσει ποσοστό της τάξης του 20% από το σύνολο των χρημάτων που παίζει το σύνολο των παικτών.

“Eye in the sky”: Με την φράση αυτή εννοούμε τους γυάλινους ή από συνθετικό υλικό (plexiglass) θόλους που βρίσκονται στην οροφή των αιθουσών του καζίνο και που σκοπό έχουν την παρακολούθηση και καταγραφή όλων όσων συμβαίνουν στους χώρους του καζίνο.

Gambler: Τζογαδόρος. Ο παίκτης που ασχολείται συστηματικά με τα τυχερά παιχνίδια, τον τζόγο (gamble).

Games of chance: Τα τυχερά παιχνίδια.

House: Αλλη λέξη για το καζίνο.

Inspector: Υπάλληλος του καζίνο υπεύθυνος για την εποπτεία μικρού αριθμού τραπεζιών παιχνιδιών. Καλείται και floorman.

Junket: Οργανωμένη ομάδα τζογαδόρων που επισκέπτονται όλοι μαζί το καζίνο.

Kibitzer: Έκφραση που χαρακτηρίζει κάποιον θεατή παιχνιδιού, ο οποίος αν και δεν συμμετέχει στο παιχνίδι εν τούτοις κάνει παρατηρήσεις και ενοχλητικά σχόλια στους παίκτες που συμμετέχουν.

Member card: Η προσωπική κάρτα που πιστοποιεί ότι ο κάτοχός της είναι μέλος του συγκεκριμένου καζίνο.

Nut: Καθορισμένο ποσό χρημάτων το οποίο ο παίκτης έχει καθορίσει ως επιδιωκόμενο κέρδος σε μια επίσκεψή του στο καζίνο.

Pit: Η περιοχή εντός μιας ομάδας τραπεζιών παιχνιδιών. Τα τραπέζια τοποθετούνται ελλειπτικά και ο χώρος εσωτερικά της περιμέτρου είναι το pit.

Pit Boss: Ο προϊστάμενος μιας συγκεκριμένης ομάδας τραπεζιών, ενός pit.

Shills: Σε καζίνο του εξωτερικού συναντάμε υπαλλήλους του καζίνο να στοιχηματίζουν σε ορισμένα παιχνίδια (π.χ. Punto Banco) υποδυόμενοι τους παίκτες, με σκοπό να προσελκύσουν πελάτες στα παιχνίδια αυτά.

Stake: Το στοίχημα. Καλείται επίσης και μίζα από την ομώνυμη γαλλική λέξη.

Table limits bets: Τα όρια στοιχημάτων που ισχύουν για ένα συγκεκριμένο τραπέζι παιχνιδιού.

*ΣΗΜΕΙΩΣΗ Υπάρχουν δύο μέθοδοι με τις οποίες εκτιμάμε την πιθανότητα ενός γεγονότος. Η κλασική μέθοδος η οποία εκτιμά ότι εάν έχουμε n διαφορετικά και εξίσου πιθανά αποτελέσματα από τα οποία τα k είναι ευνοϊκά (εάν συμβεί ένα από αυτά τότε μόνο συμβαίνει το γεγονός) η πιθανότητα του γεγονότος είναι k/n. Η άλλη μέθοδος, της σχετικής συχνότητας, εκτιμά ότι μετά από n επαναλήψεις μιας διαδικασίας με n πολύ μεγάλο, ένα γεγονός παρατηρείται ότι συνέβη k φορές, τότε η (εμπειρική) πιθανότητα του γεγονότος αυτού είναι k/n. Εξαιτίας των αδυναμιών των παραπάνω μεθόδων – ορισμών, έχει επικρατήσει μια αξιοκρατική μέθοδος θεμελίωσης της θεωρίας των πιθανοτήτων που στηρίζεται στην έννοια του δειγματοχώρου που αποτελείται από το σύνολο των δυνατών αποτελεσμάτων. Τα παραπάνω ισχύουν για ένα γεγονός. Αλλες θεωρίες έχουν αναπτυχθεί για δύο γεγονότα με όλα τα αποτελέσματα εξίσου πιθανά, για δύο γεγονότα όπου το αποτέλεσμα του δεύτερου εξαρτάται από το αποτέλεσμα του πρώτου κλπ.

Πηγές

paignio.com